| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 카카오 오픈빌더
- graphQL
- OS
- docker
- chatbot
- Mac
- vscode
- 파일권한
- jinja2
- gcp
- 카카오톡 챗봇
- 구글클라우드
- AWS
- venv
- cloud
- ssh
- 클라우드
- Windows
- Lambda
- 노션
- Python
- GQL
- 도커
- 운영체제
- 챗봇
- 시작
- flask
- braces
- nohub
- 플라스크
- Today
- Total
ForFour
PCA with eigenvector, eigenvalue 본문
핸즈온 머신러닝(2판), Data Science Handbook을 기반으로 작성되었습니다.

차원 축소: dimensionality reduction은 고차원 데이터로부터 저 차원 데이터로 변환하는 방법이다.
-위키백과
차원
흔히 물리학에서는 저차원의 생물은 상위 차원의 현상을 볼 수도 이해할 수도 없다고 이야기 합니다.
우리는 3차원 공간에 살고 있고 시간의 1축을 더해서 4차원으로 우주공간이 구성되어있다고 생각하죠. 잘은 모르지만 초끈이론과 같은 물리이론에 따르면 우주가 4차원이 아닌 더 입체적인 고차원의 차원으로 구성되어있다고 설명하고 있습니다. 아마 그런 차원의 공간은 우리는 죽었다가 깨어나도 이해하지 못할 것입니다.
하지만 데이터에서 다루는 차원은 다행히 그것보다는 비교적 훨씬 단순합니다. n차원이란 n개의 변수로 이루어진 데이터를 뜻하는 것이기 때문에 excel과 같은 테이블 형태의 데이터로 표현 가능합니다. 그럼에도 불구하고 데이터를 쉽게 이해하기 위해서는 데이터를 입체적으로 표현해야 하는데 3차원 이상의 데이터는 머릿속으로 상상하기조차 쉽지 않습니다.
초방입체 도형은 다음과 같이 그려집니다. Drawing the 4th, 5th, 6th, and 7th dimension

차원의 저주
차원이 증가한다는 것은 설명되는 변수의 개수가 증가한다는 뜻이지만 고차원의 데이터에는 매우 심각한 문제가 있습니다. 고차원에서는 그만큼 데이터를 설명할 수 있는 공간이 많다는 뜻이고 이는 즉 같은 데이터 크기라면 고차원으로 갈수록 훨씬 희소(sparse)해진다는 것을 뜻합니다.

이론적으로 단위면적에서 임의의 두 점의 거리는 평균 0.52, 1,000,000차원의 초방입체에서 무작위 두 점의 평균 거리는 약 408.25(route(1,000,000/6))이 된다고 합니다. 이를 ‘차원의 저주’라고 합니다.
차원의 저주를 해결하는 방법은 설명하는 차원을 빼곡하게 채울정도의 데이터를 확보하는 것입니다. 하지만 차원이 증가할수록 필요한 데이터는 기하급수적으로 늘어나기 때문에 현실적으로 거의 불가능합니다. 따라서 차원을 축소하는 것은 차원의 저주를 해결하는 좋은 방법이 될 수 있습니다.
특성수가 100개라고 해도, 모든 차원에 걸쳐 균일하게 퍼져 있다고 가정하고 훈련 샘플을 서로 평균 0.1 이내에 위치시키려면 관측 가능한 우주에 있는 원자 수를 모두 합친 것보다 더 많은 샘플을 모아야 합니다.
- 핸즈온 머신러닝
차원 축소 방법
차원을 축소하는 방법도 대표적으로 투영(projection) 방법과 매니폴드 학습 방법이 있습니다.
- 투영(projection): 약간의 정보 손실을 보지만 데이터를 저차원으로 투영하는 것. 투영이란 평면 혹은 차원에 수직으로 비추어 나타내는 것을 말합니다. 햇빛을 비추어 나타나는 그림자를 생각하면 편합니다.

- 매니폴드 학습: 저차원의 데이터가 고차원에 놓여있다는 가정하에 고차원 데이터를 저 차원 공간으로 풀어내는 것을 의미합니다. 대표적인 예로 스위스롤이 있습니다.

왼쪽은 위의 스위스롤 데이터를 단순히 투영시킨 것이고 오른쪽은 저 차원의 매니폴드로 압축한 모습입니다. 단순히 투영을 시킨 것은 데이터를 설명하기 어렵지만 오른쪽 그림은 설명하기 훨씬 수월합니다.

매니폴드 학습은 잘 사용되지 않는데도 다루기 까다롭고 일반적인 PCA 알고리즘보다 훨씬 느린 특징을 가지고 있습니다. 그럼에도 시각화를 하는 데는 좋은 방법이 될 수 있습니다.
PCA
PCA는 Principal Component Analysis, 주성분 분석이라고 합니다. 많이들 principle과 헷갈립니다.(principle은 원리, 원칙의 의미죠.) 차원을 축소할 때는 축소하기 전과 비교해 가장 데이터 손실이 적은 쪽을 선택해야 합니다. 그래서 분산을 이용하여 최대한 분산이 보존되는 방향으로 차원 축소를 진행합니다. 분산은 데이터가 퍼진 정도를 의미하고 다시 말하면 차원을 축소한 뒤에 분산이 가장 높은 것이 원래의 데이터를 가장 잘 설명한다고 말할 수 있습니다.
- 고유값과 고유 벡터에 대한 이해
PCA를 설명하기 위해서는 eigenvalue(고윳값)와 eigenvector(고유 벡터)에 대한 이해가 필수적입니다.
고유 벡터는 선형 변환이 일어난 후에도 방향이 변하지 않는 벡터. 즉 행렬을 가장 잘 표현한 방향. 고윳값은 그 고유 벡터에 대응하는 값을 의미합니다. 쉽게 고유벡터는 고유한 방향, 고윳값은 고유 벡터의 크기를 의미합니다.
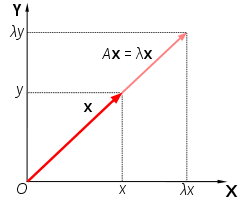
고윳값과 고유 벡터를 구하는 식은 다음과 같습니다. (det(A - λ*I) = 0)의 식에서 lambda인 고유값을 찾고 고유값을 이용해 고유값에 대응하는 고유벡터 v를 찾게됩니다. 고유벡터와 고유값을 계산하는 식은 아래와 같습니다.
*I는 단일행렬, det는 determinant 행렬식을 의미합니다. 고등학교때 배운 ad-bc, 기억하시죠?ㅎ
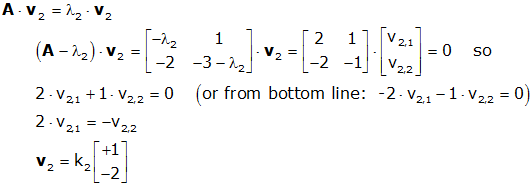
데이터에 대한 고유값과 고유벡터는 특이값 분해(svd, singular Vector Decomposition)라는 표준 행렬 분해 기술로서 주성분을 찾을 수 있습니다.
여기서 SVD는 EVD(Eigen Vector Decomposition)를 n*n 정방행렬이 아닌 n*m의 행렬에서 수행하도록 확장한 개념입니다.
SVD의 분해식은 A = U* ∑ * Vt입니다. 여기서 Vt가 주성분(고유벡터)이 됩니다. 위에서 말했듯 SVD는 정방행렬이 아닌 행렬에서도 분해가 가능하도록 확장한 개념입니다. 따라서 SVD로 분해되는 값은 단순 고유값 고유벡터를 구한 값과 다를 수 있습니다. SVD로부터 고유값 고유벡터를 유도하는 과정은 다음 영상을 참고하세요.
Computing the Singular Value Decomposition
그럼 python code로 고유값 분해가 어떻게 pca로 이어지는지 알아보겠습니다.
쉽게 1차 식으로 회귀될 수 있는 2차원 데이터를 생성하고 pca, svd를 이용한 방법으로 결과를 비교해보겠습니다. 자세한 설명은 주석을 참고해주세요.
코드를 보기전에 결과를 봅시다. 왼쪽이 생성된 랜덤 데이터 오른쪽 위가 svd를 이용한 방법, 아래가 pca library를 이용한 방법입니다.
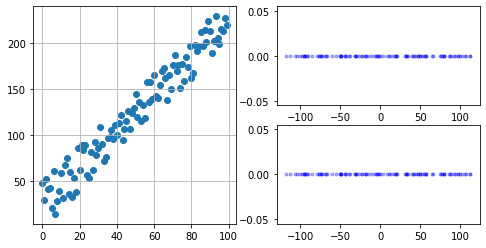
차원축소를 진행한 행렬에 대해서 svd,pca 방식이 같은 행렬을 생성한 것을 볼 수 있습니다. 다만 pca에서 결과와 방향이 다르게 나왔기 때문에 음수만 곱해주었습니다.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
# 데이터 생성
np.random.seed(4)
X = np.empty((100,2))
X[:, 0] = np.linspace(0,100,100,endpoint=False)
X[:,1] = X[:,0]*2 + np.random.random(100)*50
plt.figure(figsize=(8,4))
plt.subplot2grid((2,2),(0,0),rowspan=2)
plt.scatter(X[:,0],X[:,1])
plt.grid(True)
# sklearn의 PCA는 기본으로 평균을 빼주는 작업을 해줍니다. 우리는 SVD를 하기 전에 평균을 빼줍니다.
X_c = X-X.mean(axis=0)
U,s,Vt = np.linalg.svd(X_c)
X_reduc_svd =X_c.dot(Vt.T[:,0]).reshape(-1,1)
pca = PCA(n_components=1)
X_reduc = pca.fit_transform(X)
# pca의 결과에 -를 한 이유는 축이 반대로 뒤집혔기 때문입니다.
np.allclose(X_reduc_svd,-X_reduc) # result = True
#PCA를 한 결과와 SVD를 이용한한 결과가 완전히 똑같은 것을 볼 수 있습니다다.
plt.subplot2grid((2,2),(0,1))
plt.plot( X_reduc_svd, np.zeros(100),'b.',alpha=0.3)
#plt.plot( X2D, np.zeros(100),'b.',alpha=0.3)
plt.subplot2grid((2,2),(1,1))
plt.plot(-X_reduc, np.zeros(100),'b.',alpha=0.3)
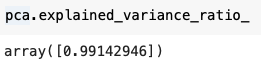
Sklearn의 PCA는 explained_variance_pratio_라는 속성을 통해 각 주성분마다 포함하고 있는 분산의 비율을 알 수 있습니다. 위의 PCA 결과는 약 99%의 분산을 유지한 채 차원축소 된 것을 알 수 있습니다.
압축과 복원
PCA를 하는 것은 위와같이 일부 데이터를 손해보면서 압축시키는 것입니다. 그리고 압축된 값은 다시 역연산을 통해 복원시킬 수 있습니다. 역변환은 pca.inverse_transform(X_reduc)으로 가능합니다.
PCA 친구들
- Randomized PCA: 일반 PCA보다 빠르게 d차원의 주성분 근사치를 찾습니다. 줄이려는 차원수(d)가 원래 차원(N)보다 많이 작을 때 효과적으로 빠른 성능을 보여줍니다.
- Incremental PCA: 점진적 PCA입니다. PCA를 진행하려면 데이터를 메모리에 올려야하는데 큰 데이터 셋은 한번에 데이터를 메모리에 올리기 힘들 수 있습니다. 이때 배치사이즈만큼씩 pca를 할 수 있게 해줍니다.
- kernel PCA: kernel 기술은 오히려 차원축소와는 다르게 오히려 차원을 늘리는 기술입니다. kernel을 통해 쉽게 선형으로 분리할 수 없는 XOR 데이터를 쉽게 분리할 수 있도록 도와줍니다. kernel PCA는 kernel 기술을 사용한 후 PCA를 진행하는 방법입니다. kernel PCA를 이용해 복잡한 비선형 투영을 수행할 수 있도록 해줍니다.
- MDS: 다차원 스케일링. MDS는 샘블단의 거리를 보존하면서 차원을 축소합니다.
- LLE: Locally Linear embedding입니다. LLE는 가장 가까운 이웃에 선형적으로 연관되어있는지 측정하여 차원을 축소하는 기술입니다. MDS는 모든 요소의 거리를 보존하지만 LLE는 가까운 거리에 있는 이웃 n개에 대해 고려합니다.
'kaggle & ML' 카테고리의 다른 글
| [kaggle]심슨 캐릭터 인식하기 - additional(삽질과 모델 개선) (0) | 2021.11.28 |
|---|---|
| [kaggle]심슨 캐릭터 인식하기(The Simpsons character recongnition) (0) | 2021.11.28 |


